Intrinsic Neural Fields: Learning Functions on Manifolds

Lukas Koestler, Daniel Grittner, Michael Moeller, Daniel Cremers, Zorah Lähner

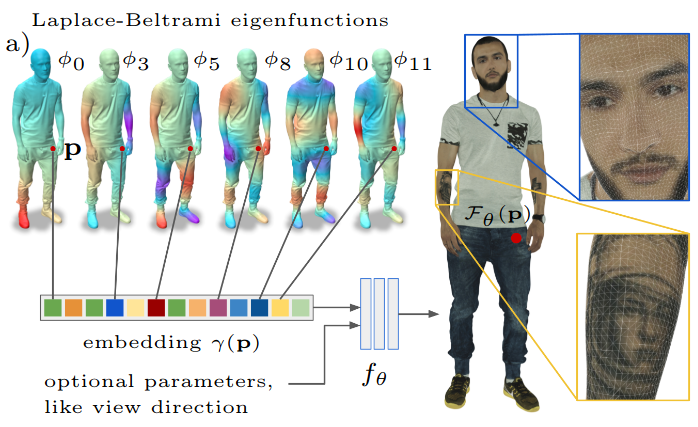
Abstract

Many applications require the robustness, or ideally the invariance, of a neural network to certain transformations of input data. Most commonly, this requirement is addressed by either augmenting the training data, using adversarial training, or defining network architectures that include the desired invariance automatically. Unfortunately, the latter often relies on the ability to enlist all possible transformations, which make such approaches largely infeasible for infinite sets of transformations, such as arbitrary rotations or scaling. In this work, we propose a method for provably invariant network architectures with respect to group actions by choosing one element from a (possibly continuous) orbit based on a fixed criterion. In a nutshell, we intend to ‘undo’ any possible transformation before feeding the data into the actual network. We analyze properties of such approaches, extend them to equivariant networks, and demonstrate their advantages in terms of robustness as well as computational efficiency in several numerical examples. In particular, we investigate the robustness with respect to rotations of images (which can possibly hold up to discretization artifacts only) as well as the provable rotational and scaling invariance of 3D point cloud classification.

Resources

[pdf] [arxiv] [github]

Bibtex

@inproceedings{koestler2022intrinsic,
    author 	= {Lukas Koestler and Daniel Grittner and Michael Moeller and Daniel Cremers and Zorah L\"ahner},
    title 	= {Intrinsic Neural Fields: Learning Functions on Manifolds},
    booktitle   = {European Conference on Computer Vision (ECCV)},
    year 	= "2022",
}